11118. Монетки

Пока Мелман сидел в узком ящике и куда-то плыл, ему было очень скучно. Чтобы себя чем-то развлечь, он начал играть в игру с n монетками, которые нашел в ящике.

Он положил монетки перед собой в ряд и пронумеровал их от 1 до n слева направо. Некоторые монетки лежат вверх решкой, а некоторые – орлом. Затем, Мелман начинает делать ходы. Для начала он считает число k – количество монеток, лежащих орлом вверх. Если таких монет нет, то игра заканчивается. Иначе, он делает ход – переворачивает монетку номер k.

Помогите Мелману по начальному расположению монеток определить, сколько раз ему придется сделать ход, чтобы закончить игру. Либо сообщите, что игра будет длиться бесконечно долго.

Вход. В первой строке дано одно целое число n (1 ≤ n ≤ 10⁵) – количество монеток. В следующей строке дана строка из n символов “0” и “1” – начальное расположение монеток. Символ “0” соответствует монетке, лежащей вверх решкой, а символ “1” орлом.

Выход. Если игра будет длиться бесконечно, выведите “-1”. А иначе, выведите количество ходов, которые Мелману придется сделать перед тем, как игра закончится.

Пример входа 1	Пример выхода 1
5 00101	12
Пример входа 2	Пример выхода 2
3 101	4

РЕШЕНИЕ

моделирование

Анализ алгоритма

Пусть k – количество единиц. Рассмотрим инвертирование элемента на позиции k. До инвертирования всегда будет существовать элемент на позиции, не меньшей k, равный 1. Пусть этот элемент находится на позиции q.

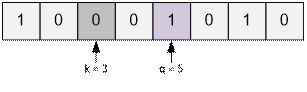
Сначала заменим 0 на 1 в позиции k. После чего k увеличится на 1. Если k < q, то снова заменим 0 на 1 в позиции k и увеличим k на 1. И так далее: заменим 0 на 1 q – k раз на позициях [k; q).

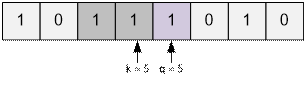
Теперь поменяем на позиции q единицу на ноль.

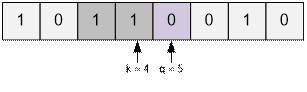
Затем еще q – k раз заменим 1 на 0 на позициях [k; q) двигаясь справа налево.

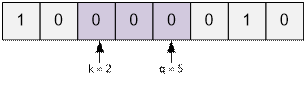
Таким образом мы сделали (q – k) * 2 + 1 операций, после чего количество единиц уменьшилось на 1. Следовательно процесс всегда конечный.

Вo множестве indexes будем поддерживать позиции единиц. За одну итерацию будем обрабатывать удаление одной единицы. Для этого считаем текущее число единиц k. Находим позицию с единицей, не меньшую k, пусть ею будет q. Увеличиваем ответ – количество проделанных операций – на (q – k) * 2 + 1.

Реализация алгоритма

Объявим множество indexes, в котором будем поддерживать позиции единиц.

set<int> indexes;

Читаем входные данные. Во множестве indexes сохраняем позиции единиц. В переменной k подсчитываем их количество.

cin >> n >> s;

k = 0;

for (i = 0; i < n; i++)

if (s[i] == '1')

{

indexes.insert(i + 1);

k++;

}

В переменной res будем подсчитывать искомое количество ходов.

long long res = 0;

while (!indexes.empty())

{

Ищем позицию first_right единицы, не меньшей k.

first_right = indexes.lower_bound(k);

Прибавляем к ответу res количество ходов, необходимых для удаления одной единицы.

res += (*first_right - k) * 2 + 1;

Удаляем позицию удаленной единицы.

indexes.erase(first_right);

Уменьшаем на 1 количество имеющихся единиц k.

k--;

}

Выводим ответ.

cout << res << '\n';